Batch 3 - Class 194 - Parity
Pre-Class Exercise
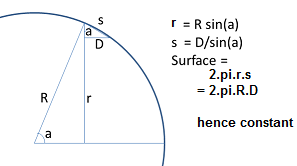
If we slice one half of a perfectly rounded loaf of bread into equal width slices, which piece has the most crust? Why?
- Answer: For each slice starting from the largest (middle) slice going outwards, the increase in surface width is same as reduction in slice size (determined by radius of slice). Hence the surface area of the crust is the same.
- For those who understand trigonometry,
Attendance Mahi, Muskaan, Rohan, Rehan, Siddhant, Anshi, Aashvi, Angad
Class puzzles
- (MC Chap 1, Prob 8) Can a 5x5 square checkerboard be covered by 1x2 dominos?
- Answer: No; Follow up - mutilated 6x6 chessboard with opposite corners removed
Instructor Notes: Ensure kids see the number of colored and white squares and why it can't be done
- (MC Chap 1, Prob 1) Eleven gears are placed in a plane, connected to each other in a circle. Can all gears rotate simultaneously?
- Answer: No; Clockwise and anticlockwise gears have to alternate
- (MC Chap 1, Prob 6) Mahika and her friends are standing in a circle, such that both neighbors of each child are of the same gender. If there are 5 boys in the circle, how many girls are there?
- Answer: 5; alternate
Instructor Notes: Kids tend to get the alternate pattern, but may not be able to prove that thats the only option. Work with them to show what happens if there are two boys or two girls next to each other.
- Can kids identify some things that are always even or odd, or always go from even to odd and odd to even?
- Always even - multiply by 2
- Always odd - multiply by 3
- Even -> Odd -> Even ... - normal counting
- (MC Chap1, Prob 3) Can a knight start at square a1 of the chessboard, and go to h8, visiting each square exactly once?
- Answer: No. There are 63 moves in all, and the knight changes color of cell in each move. So if it starts from a white square, it must end up on a black one.
Instructor Note: Let kids discover the black/white parity, and the fact these alternate. Hence 63 moves can not bring it back to same color.
- (MC Chap 1, Prob 5) Three hockey pucks A, B, C lie on playing field. A player hits one of them so that it passes between the other two. He does this 25 times. Can he return the pucks to their starting point?
- Answer: No. In each move the ABC circle (arbitrarily chosen) goes from clockwise to anti-clockwise or vice-versa. So in odd moves, you cant come back to original position.
Instructor Note: Let kids discover the notion of clockwise and anti-clockewise parity?
- (MC Chap 1, Prob 31) Of 101 coins, 50 are counterfeit and differ from genuine coins by 1gm (positive or negative). There is a balance which shows difference in weight on two pans. You choose 1 coin and want to determine in one weighing if it is genuine or counterfeit
- Answer: Weight remaining 50 against 50. Regardless of the mix, if the difference is even, then the coin outside is genuine, else fake
Instructor Notes: Try working with smaller numbers. If they are not able to get it, try working with simpler case that all fake are positive 1gm.
Homework
- (Khan Academy) 10 prisoners are given a chance of survival by the jailer. The jailer tells them that the next morning, he will have them stand in a queue (so that the last person can see the nine people in front, the second last people can see eight people in front of him, and so on), and then place either a red hat or a purple hat on each person's head. The person hence will be able to see the color of hat for people in front of him (but not his own hat). The jailer will then start from the last person, and ask each person "What is the color of hat on your head". The person can answer "red" or "purple". If the person's answer is correct, he will be released, else he will be killed. The jailer will then ask the same question to the second last person, and so on. The prisoners have the night to figure out the strategy so that maximum number of prisoners can survive (on a guaranteed basis). Figure out a strategy to save the maximum number of prisoners.
- Answer: "Last guy calls the odd number of hats in front". Every person there on keeps a count of odd or even parity.
Instructor Notes: Take example to explain, let kids do it, try for smaller number to illustrate induction, parity thinking
References:
Mathematical Circles (Russian Experience), by Dmitri Fomin, Sergey Genkin, Ilia Itenberg
The Colossal Book of Short Puzzles and Problems, by Martin Gardner
Khan Academy - https://www.khanacademy.org/math/recreational-math/brain-teasers/v/alien-abduction-brain-teaser